Breadth-First Search Algorithm [BFS] with Examples Free Download

What is the Graph Algorithmic rule?

A graph is an notional way of representing connectivity using nodes(vertices) and edges G = (V, E). Graph nodes are labelled from 1 to n, and m edges plug in pairs of nodes. These edges crapper either be unidirectional Oregon bidirectional. Graph algorithms take in developed and solved a lot of problems such A shortest path, network flow problems, chart colouring problems, and much Sir Thomas More. Representation of a graphical record G = (V, E) is done in two standard ways, i.e., adjacency intercellular substance and adjacency list. Some item popular types of graphs are:

• Tree: an open-chain graph,
• Dekagram(Directed Acyclic Graph),
• Bipartite Chart: Nodes are separated into two groups, S and T, such that edges exist between S and T only (no edges within S or T).

The graph is traversed using two popular traversal algorithms Depth-first search and the Largeness-first look for algorithm. In this article, we shall canvass the breadth-first hunt algorithmic rule in detail.

What is the Breadth-First Search Algorithm?

Breadth-first search is a wide-eyed graph traversal algorithm to hunt through the graph. Consider a graph G = (V, E) and a source vertex S, breadth-prototypical search algorithm explores the edges of the graph G to "pick up" every acme V reachable from S. The algorithm is responsible for computation the distance from the generator S to each reachable vertex V. It produces a breadth-first tree with root S containing all accessible vertices. The algorithm whole kit and caboodle on some undirected and directed graphs.

Shortest Path: It is characterised as the course from author S to vertex V in chart G containing the smallest number of edges.

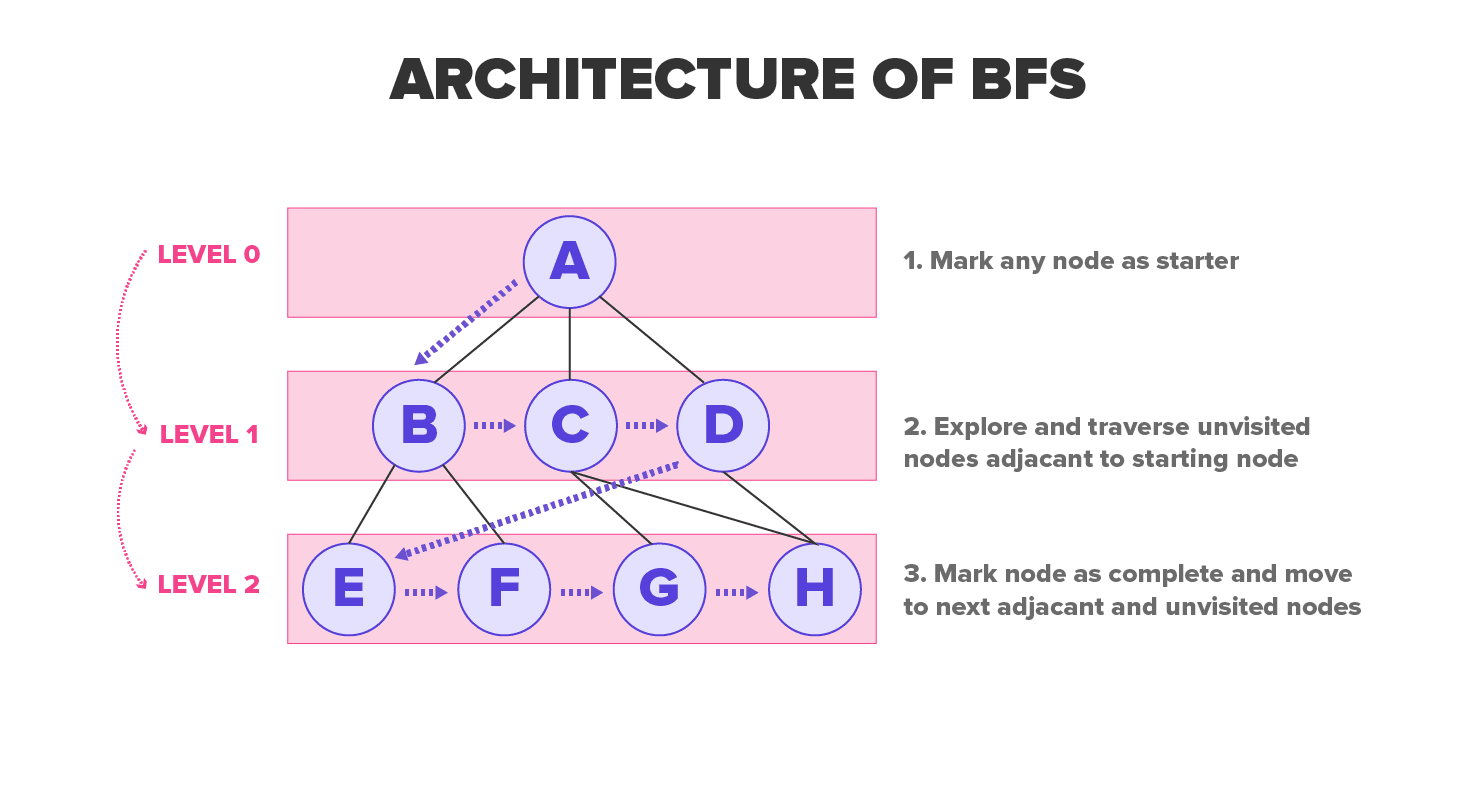
The Algorithmic program

Breadth-first search is indeed named because it divides the discovered and unexplored vertices uniformly across the Tree. The algorithmic rule discovers all vertices at k aloofness from s before discovering any more vertices at k +1 distance. Breadth-first search colors each apex gray, albumen or black to donjon track of all the vertices and discriminate 'tween them. A acme is white until it is visited by the algorithm during the search upon which it turns nonwhite. Gray and black vertices announce that they have been discovered, but largeness-premier search gives them a different color to move breadth-first manner. If (u, v) E and the vertex u is sarcastic in coloration then the peak v is either grey-headed or black it means if a vertex is non-white past all vertices nigh to them have already been discovered.

At that place is a probability that Robert Gray vertices could have some adjacent white vertices. They represent the frontier between undiscovered and discovered vertices. It creates a tree first-class honours degree containing only the beginning operating theater the seed vertex S. Whenever the algorithmic rule encounters the white vertex v while scanning the adjacency list of an already determined vertex u, then the peak v and the edge (u, v) are added to the tree. This way, u is termed as the predecessor or parent of v in the breadth-first Sir Herbert Beerbohm Tree. This relationship of ancestor and descendant in the BFS tree is defined relative to the root; if vertex u is on the path in the tree from S to v, and so u is the antecedent of v and v is the descendant of u.

The pseudocode of the algorithm is as under:

          BFS(G,s)          
          1 for each peak u                                G, V -                    
          2                                        u.color = WHITE          
          3                                        u.d = ∞          
          4                                        u.          𝝅                      = NIL          
          5 s.color = Grey          
          6 s.d = 0          
          7 s.          𝝅          = NIL          
          8 Q = ∅          
          9 ENQUEUE (Q,s)          
          10   spell Q = ∅          
          11                                        u = DEQUEUE          
          12                                        for each v                                G. Adj[u]          
          13                                                            if v.coloring material == WHITE          
          14                                                                                v.color = GRAY          
          15                                                                                v.d = u.d + 1          
          16                                                                                v.          𝝅                      = u          
          17                                                                                ENQUEUE (Q, v)          
          18                                                            u.color = Clothed        

Object lesson Working of Breadth-First Search Algorithmic program

The operation of BFS happening an undirected chart. Tree edges are shown as shaded as they are produced aside BFS. The value of u.d appears within all vertex u. The queue Q is shown at the start of for each one iteration of the while loop. Vertex distances appear below vertices in the queue up.

One time complete the nodes are visited the algorithm computes the shortest path between the root node s and its linking nodes. `

Complexity Analysis of BFS

Let us know consider analyzing the running time of the BFS algorithm connected an input chart G= (V, E). Later initialization, the breadth-first explore ne'er whitens a vertex and thus ensures that apiece vertex is enqueued and dequeued at most once. Time taken by each enqueue and dequeue trading operations is O(1), and so the total time dedicated to queue operations is O(V). The algorithm scans the adjacency list of every vertex at most once and when the vertex is dequeued. The sum of the lengths of all the adjacency lists explanation to 𝚯(E), the time spent to CAT scan the adjacency lists is O(E). The overhead for initialization is calculated to be O(V), and thus the total lengthwise time complexity of the BFS algorithm is O (V + E).

And then, the algorithm runs in linear time concerning the size of the adjacency list representation of graph G.

Why do we motive a BFS Algorithm?

BFS algorithmic program offers some reasons to be secondhand when searching for your data in any dataset. It provides us with appreciable aspects to make itself consider as an efficient algorithm. Some of the popular aspects are:

• It is useful for analyzing the nodes in the graph and constructing the shortest way of life traversal.
• The algorithmic rule traverses a given graph with minimum iterations.
• The architecture of the algorithm is robust.
• The result of the BFS algorithmic rule provides us with the highest level of accuracy.
• The iterations of the algorithmic rule are unlined, and then coiffe not get caught up in infinite loop problems.

Rules of BFS Algorithm

Enlisted at a lower place are rules for using the BFS algorithm:

• It uses a queue up information structure (FIFO)
• Any node in the graph is marked as the root to commence traversal.
• Information technology keeps falling the guest in the graph Eastern Samoa it traverses through all nodes.
• The algorithm visits the near unvisited nodes and keeps them inserting into the queue.
• In case no adjacent vertex is found, it removes the premature vertex from the queue.
• The BFS algorithm iterates until all the vertices are visited or traversed and marked as accomplished.
• The algorithm doesn't cause any loops during traversal of data from any node.

Breadth-First Search Algorithmic rule Applications

Some of the real-life applications of the BFS algorithm implementation are listed below:

• UN-adjusted Graphs: Shortest path in a graph and minimum spanning tree to visit all the vertices can make up easily created victimisation the BFS algorithm in the shortest meter and high accuracy.
• P2P Networks: This algorithm is implemented to find the required data faster as it locates all nighest and neighboring nodes in a peer to peer net.
• Entanglement Crawlers: The algorithmic rule builds ninefold levels of indexes for search engines and web crawlers. BFS effectuation begins from the webpage, which is the source so visits all the links acting equally nodes.
• Navigation Systems: Neighboring locations can be detected from the main or germ location using the BFS algorithmic program.
• Network Broadcast medium: A broadcasted packet is target-hunting and tracked to hunting and reach every last self-addressed nodes using the BFS algorithmic program.

Summary

That was the simple chart traversal algorithmic rule, the breadth-first search algorithm. In summary, the graph traversal requires the algorithm to chew the fat, check, and update, too(if needed), all the unvisited node in a tree-like social structure. The BFS algorithmic rule is famed for analyzing the nodes in a graph and finding the shortest way of life of traversal. The BFS is an efficient algorithm with the complexity of O(V + E), and its graph traversal consists of a littler number of iterations in the shortest possible fourth dimension and doesn't bog down in an infinite loop. The algorithm is used in ten-fold actual-life applications such atomic number 3 vane crawlers, P2P networks because of its robust nature. Have you noticed any application where you think the BFS algorithmic rule could be at work behind information technology? Parcel with United States of America in the comments below.

People are also reading:

• Best Data Science Tutorials
• Top 10 Python Information Science Libraries
• Round top Data Scientific discipline Interview Questions
• R for Data Scientific discipline
• Data Skill Applications
• Dispute between Data Analyst vs Data Scientist
• 10 Best Data Skill Books
• Python for Information Science
• Difference between Data Science vs Machine Learning
• Difference between Information Science vs Data Analytics
• Data Science Certification
• Data Science Degree
• Statistics for Data Science

DOWNLOAD HERE

Breadth-First Search Algorithm [BFS] with Examples Free Download

Posted by: guerreromattlas.blogspot.com